Tìm hiểu Mô đun math trong Python: Các hàm toán học, lượng giác, hằng số và ví dụ code thực tế

Giới thiệu về mô đun math trong Python

Bạn có biết Python tích hợp sẵn mô đun math giúp giải quyết các phép tính toán học phức tạp? Khi làm việc với các dự án lập trình, chúng ta thường gặp phải những bài toán đòi hỏi tính toán toán học chính xác và hiệu quả. Vấn đề khi tính toán thủ công hoặc tự viết hàm toán học thường gây rắc rối, không hiệu quả và dễ mắc lỗi sai số.

Mô đun math là giải pháp nhanh chóng, chính xác hỗ trợ nhiều hàm và hằng số toán học phổ biến. Đây là một trong những thư viện chuẩn của Python, có nghĩa là bạn không cần cài đặt thêm bất cứ gói nào khác. Chỉ cần một dòng lệnh import đơn giản, bạn đã có thể truy cập vào kho tàng các công cụ toán học mạnh mẽ.

Bài viết này sẽ tổng quan về cách import mô đun math, các hàm phổ biến nhất, hằng số quan trọng, ví dụ thực tế với code mẫu và so sánh với các thư viện khác như NumPy. Mục tiêu của chúng ta là giúp bạn nắm vững mô đun math và áp dụng hiệu quả vào các dự án Python của mình.

Các hàm toán học phổ biến trong mô đun math

Hàm xử lý căn bậc hai, lũy thừa và làm tròn

Trong lập trình hàng ngày, chúng ta thường xuyên cần thực hiện các phép tính cơ bản như tính căn bậc hai, lũy thừa và làm tròn số. Mô đun math cung cấp những hàm này với độ chính xác cao và hiệu suất tối ưu.

Hàm sqrt(x) giúp tính căn bậc hai của một số. Ví dụ, math.sqrt(16) sẽ trả về 4.0. Đây là hàm rất hữu ích khi bạn cần tính khoảng cách giữa hai điểm trong hình học hoặc tính độ lệch chuẩn trong thống kê.

Hàm pow(x, y) tính lũy thừa x^y. Mặc dù Python có toán tử ** để tính lũy thừa, nhưng math.pow() trả về kết quả dạng số thực (float) và xử lý các trường hợp đặc biệt tốt hơn. Ví dụ: math.pow(2, 3) trả về 8.0.

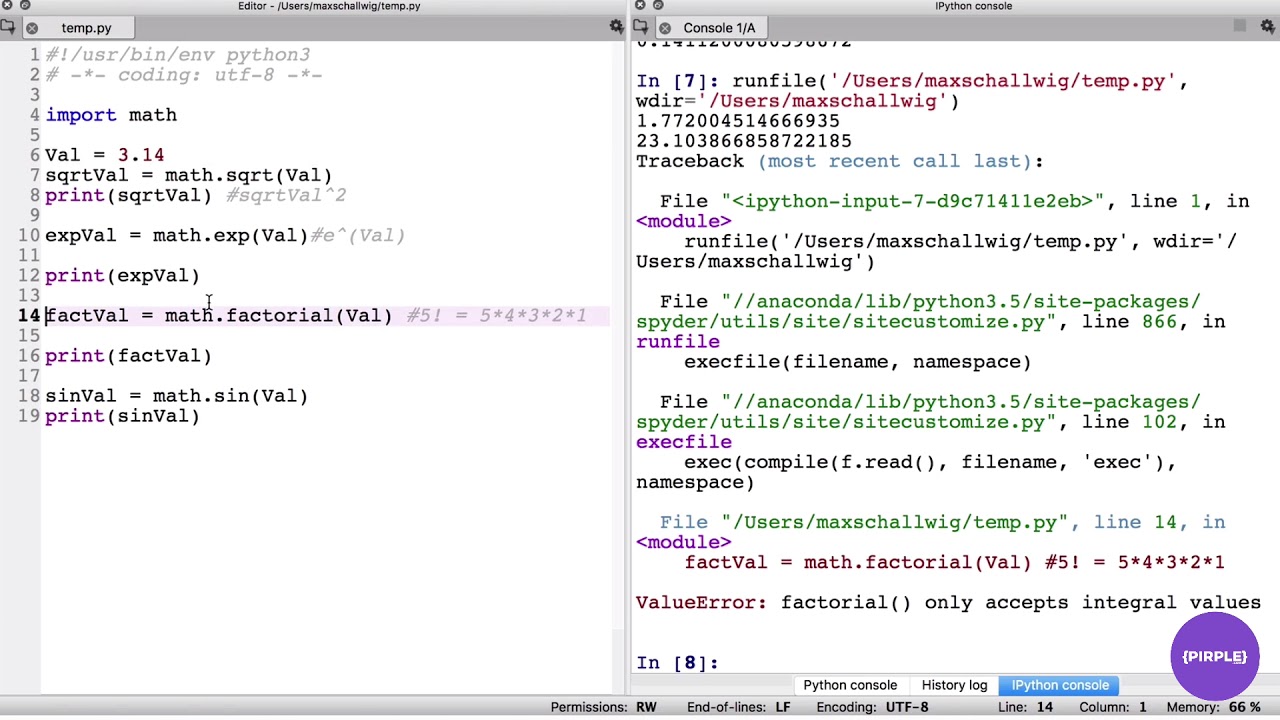
Đối với việc làm tròn, chúng ta có ceil(x) và floor(x). Hàm ceil(x) làm tròn lên số nguyên gần nhất, trong khi floor(x) làm tròn xuống. Điều này rất hữu ích khi bạn cần xử lý số lượng sản phẩm, trang web, hoặc bất kỳ giá trị nào cần phải là số nguyên.

Hàm mũ và logarit

Các hàm mũ và logarit đóng vai trò quan trọng trong nhiều thuật toán và phép tính khoa học. Hàm exp(x) tính e mũ x, trong đó e là hằng số Euler (khoảng 2.718). Đây là hàm cực kỳ quan trọng trong toán học và có ứng dụng rộng rãi trong machine learning, tài chính và vật lý.

Hàm log(x[, base]) tính logarit của x. Nếu không chỉ định base, hàm sẽ tính logarit tự nhiên (cơ số e). Bạn có thể chỉ định cơ số khác như math.log(100, 10) để tính logarit cơ số 10 của 100, kết quả là 2.0. Logarit rất hữu ích trong xử lý dữ liệu, đặc biệt khi cần chuyển đổi thang đo hoặc giảm độ lớn của các giá trị.

Các hàm lượng giác và hằng số toán học quan trọng

Hàm lượng giác cơ bản

Lượng giác là một phần không thể thiếu trong lập trình đồ họa, game development và các ứng dụng mô phỏng. Mô đun math cung cấp đầy đủ các hàm lượng giác cơ bản: sin(x), cos(x), và tan(x).

Điều quan trọng cần nhớ là các hàm này nhận đầu vào theo đơn vị radian, không phải độ. Ví dụ, để tính sin của 30 độ, bạn cần chuyển đổi: math.sin(math.radians(30)) hoặc math.sin(30 * math.pi / 180). Kết quả sẽ là 0.5, đúng như chúng ta mong đợi.

Các hàm lượng giác này cực kỳ hữu ích khi bạn làm việc với đồ họa 2D/3D, tính toán quỹ đạo, hoặc tạo hiệu ứng sóng trong game. Chúng cũng được sử dụng rộng rãi trong xử lý tín hiệu số và phân tích dữ liệu chu kỳ.

Hằng số pi và e

Mô đun math cung cấp hai hằng số toán học quan trọng nhất: math.pi và math.e. Hằng số π (pi) có giá trị khoảng 3.14159 và được sử dụng trong tất cả các phép tính liên quan đến hình tròn, hình cầu và các phép tính lượng giác.

Hằng số e (số Euler) có giá trị khoảng 2.71828 và là cơ số của logarit tự nhiên. Đây là một trong những hằng số quan trọng nhất trong toán học, xuất hiện trong nhiều công thức về tăng trưởng mũ, xác suất và thống kê.

Ví dụ thực tế với code mẫu và kết quả

Ví dụ tính toán căn bậc hai và lũy thừa

Hãy xem một ví dụ thực tế về cách sử dụng các hàm math trong Python:

import math

# Tính khoảng cách giữa hai điểm (x1, y1) và (x2, y2)
def tinh_khoang_cach(x1, y1, x2, y2):
    return math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))

# Ví dụ sử dụng
diem_A = (0, 0)
diem_B = (3, 4)
khoang_cach = tinh_khoang_cach(diem_A[0], diem_A[1], diem_B[0], diem_B[1])
print(f"Khoảng cách giữa điểm A và B là: {khoang_cach}")  # Kết quả: 5.0

Trong ví dụ này, chúng ta sử dụng định lý Pythagoras để tính khoảng cách giữa hai điểm. Hàm math.pow() tính bình phương của hiệu các tọa độ, sau đó math.sqrt() lấy căn bậc hai của tổng. Đây là hàm trong Python hữu ích trong việc tái sử dụng mã và tổ chức logic tính toán hiệu quả.

Ví dụ sử dụng hàm lượng giác trong bài toán

Dưới đây là ví dụ về cách sử dụng hàm lượng giác để tính toán vị trí của một điểm trên đường tròn:

import math

def vi_tri_tren_duong_tron(ban_kinh, goc_do):
    # Chuyển đổi từ độ sang radian
    goc_rad = math.radians(goc_do)
    
    # Tính tọa độ x, y
    x = ban_kinh * math.cos(goc_rad)
    y = ban_kinh * math.sin(goc_rad)
    
    return x, y

# Ví dụ: điểm trên đường tròn bán kính 10 tại góc 45 độ
x, y = vi_tri_tren_duong_tron(10, 45)
print(f"Vị trí: x = {x:.2f}, y = {y:.2f}")  # Kết quả: x = 7.07, y = 7.07

Các tình huống sử dụng phổ biến mô đun math

Mô đun math được sử dụng rộng rãi trong nhiều lĩnh vực lập trình khác nhau. Trong tính toán khoa học và kỹ thuật, các hàm math giúp thực hiện các phép tính phức tạp một cách chính xác và hiệu quả. Ví dụ, trong mô phỏng vật lý, bạn cần tính toán quỹ đạo, vận tốc, gia tốc – tất cả đều yêu cầu các hàm toán học.

Trong xử lý dữ liệu và các bài toán tài chính, thống kê đơn giản, mô đun math cung cấp những công cụ cần thiết để tính toán lãi suất kép, phân tích xu hướng, hoặc chuẩn hóa dữ liệu. Đặc biệt, các hàm logarit rất hữu ích trong việc xử lý dữ liệu có thang đo lớn hoặc tăng trưởng mũ.

Một lợi thế lớn của mô đun math là nó tích hợp sẵn trong Python, không cần cài đặt thêm thư viện bên ngoài. Điều này giúp ứng dụng của bạn nhẹ nhàng hơn và dễ triển khai hơn, đặc biệt quan trọng khi làm việc với các môi trường có hạn chế về tài nguyên.

So sánh mô đun math với các thư viện tính toán khác như NumPy

Khi nào bạn nên sử dụng mô đun math và khi nào nên chuyển sang NumPy? Đây là câu hỏi mà nhiều developer Python thường đặt ra. Mô đun math nhẹ, tích hợp sẵn và phù hợp cho các phép tính đơn giản trên từng số riêng lẻ. Nó không hỗ trợ xử lý mảng hay vector, nhưng lại có ưu điểm là không tạo thêm dependency cho dự án.

Ngược lại, NumPy mạnh mẽ hơn nhiều với khả năng hỗ trợ mảng đa chiều, thích hợp cho xử lý dữ liệu lớn và tính toán vectorized. NumPy có thể thực hiện cùng một phép tính trên hàng nghìn phần tử cùng lúc, trong khi math chỉ xử lý từng số một.

Quy tắc đơn giản: sử dụng math khi bạn cần thực hiện các phép tính đơn giản, không cần xử lý mảng, và muốn giữ ứng dụng nhẹ. Chuyển sang NumPy khi bạn làm việc với dữ liệu lớn, cần tính toán trên mảng, hoặc phát triển ứng dụng khoa học/machine learning. Cả hai thư viện đều có vị trí riêng trong hệ sinh thái Python và bổ sung cho nhau rất tốt.

Các vấn đề thường gặp và cách khắc phục

Lỗi import mô đun math

Mặc dù math là thư viện chuẩn, đôi khi bạn vẫn có thể gặp lỗi import. Nguyên nhân phổ biến nhất là xung đột tên file. Nếu bạn đặt tên file Python của mình là “math.py”, nó sẽ ghi đè lên mô đun math gốc và gây ra lỗi circular import.

Cách khắc phục: đổi tên file của bạn thành tên khác, xóa file math.pyc nếu có, và khởi động lại Python interpreter. Luôn tránh đặt tên file trùng với tên các mô đun chuẩn của Python.

Sai số hoặc hiểu nhầm về đơn vị trong hàm lượng giác

Lỗi phổ biến nhất khi sử dụng hàm lượng giác là nhầm lẫn giữa độ và radian. Tất cả hàm lượng giác trong mô đun math đều sử dụng radian làm đơn vị đầu vào. Nếu bạn có góc theo độ, cần chuyển đổi bằng math.radians(goc_do) hoặc goc_do * math.pi / 180.

Tương tự, khi muốn chuyển từ radian về độ, sử dụng math.degrees(goc_rad) hoặc goc_rad * 180 / math.pi. Việc nhớ điều này sẽ giúp bạn tránh được nhiều lỗi tính toán không mong muốn.

Best Practices khi sử dụng mô đun math trong Python

Để sử dụng mô đun math hiệu quả, hãy áp dụng những best practices sau. Đầu tiên, luôn import mô đun math ở đầu file code để dễ quản lý và maintain. Sử dụng import math thay vì from math import * để tránh xung đột tên và làm code rõ ràng hơn.

Kiểm tra kỹ đơn vị đầu vào cho hàm lượng giác. Luôn chú ý xem bạn đang làm việc với độ hay radian, và chuyển đổi khi cần thiết. Điều này sẽ giúp tránh những lỗi tính toán khó phát hiện.

Sử dụng các hàm có sẵn thay vì viết lại thủ công. Các hàm trong mô đun math đã được tối ưu hóa về hiệu suất và độ chính xác. Việc tự implement lại không chỉ tốn thời gian mà còn dễ gây ra lỗi sai số.

Cuối cùng, không nên dùng mô đun math cho xử lý mảng lớn. Khi cần tính toán trên nhiều phần tử cùng lúc, hãy chuyển sang NumPy để tối ưu tốc độ và hiệu suất.

Kết luận

Mô đun math là công cụ mạnh mẽ, dễ sử dụng cho hầu hết nhu cầu tính toán cơ bản trong Python. Từ những phép tính đơn giản như căn bậc hai, lũy thừa cho đến các hàm lượng giác phức tạp, mô đun math cung cấp đầy đủ những gì bạn cần để giải quyết các bài toán toán học trong lập trình.

Hiểu rõ các hàm và hằng số trong mô đun math giúp bạn viết code nhanh, chính xác và dễ bảo trì. Những kiến thức này không chỉ hữu ích trong công việc hàng ngày mà còn là nền tảng vững chắc cho những dự án phức tạp hơn về sau.

Hãy bắt đầu thử nghiệm với các ví dụ đơn giản từ bài viết này và dần dần mở rộng lên các bài toán phức tạp hơn. Thực hành là cách tốt nhất để nắm vững kiến thức và phát triển kỹ năng lập trình.

Đừng quên áp dụng các best practices mà chúng tôi đã chia sẻ và thường xuyên tham khảo tài liệu chính thức của Python để cập nhật những tính năng mới. Với mô đun math làm công cụ đắc lực, bạn sẽ tự tin hơn khi giải quyết những thử thách lập trình liên quan đến tính toán toán học.

Chia sẻ Tài liệu học Python