Recursion trong Python: Hiểu cơ chế, ví dụ thực tế và lưu ý quan trọng

Giới thiệu về đệ quy trong Python

Bạn đã bao giờ tự hỏi liệu một hàm trong Python có thể gọi lại chính nó không? Câu trả lời là có, và kỹ thuật này được gọi là đệ quy (recursion). Đệ quy là một trong những khái niệm quan trọng nhất trong lập trình, giúp chúng ta giải quyết các bài toán phức tạp bằng cách chia nhỏ thành những phần đơn giản hơn.

Tại sao đệ quy lại quan trọng đến vậy? Đơn giản vì nó giúp chúng ta tiếp cận bài toán theo cách trực quan và tự nhiên. Thay vì phải suy nghĩ phức tạp về vòng lặp, chúng ta chỉ cần tập trung vào việc định nghĩa bài toán nhỏ hơn. Điều này đặc biệt hữu ích khi làm việc với cấu trúc dữ liệu như cây, đồ thị, hoặc các bài toán chia để trị.

Trong bài viết này, tôi sẽ dẫn bạn khám phá đệ quy từ những khái niệm cơ bản nhất. Chúng ta sẽ cùng tìm hiểu định nghĩa, cách hoạt động, các ví dụ thực tế với code minh họa chi tiết, những vấn đề thường gặp phải, và cuối cùng là những best practices để sử dụng đệ quy hiệu quả. Mục tiêu là giúp bạn không chỉ hiểu mà còn có thể áp dụng thành thạo kỹ thuật này trong các dự án thực tế.

Định nghĩa và cơ chế hoạt động của đệ quy

Đệ quy là gì?

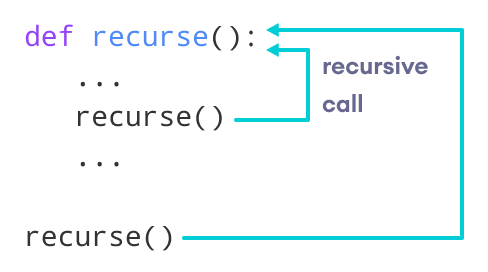
Đệ quy trong Python là một kỹ thuật lập trình mà trong đó một hàm sẽ gọi lại chính nó với dữ liệu đầu vào được rút gọn dần, cho đến khi đạt được điều kiện dừng (base case). Hãy tưởng tượng đệ quy như một cái gương phản chiếu vào nhau – mỗi lần phản chiếu là một lần gọi hàm, và chúng ta cần có điểm dừng để tránh phản chiếu vô hạn.

Tại sao đệ quy lại quan trọng trong lập trình? Đầu tiên, nó giúp đơn giản hóa các bài toán phức tạp bằng cách chia nhỏ thành những phần dễ giải quyết hơn. Thứ hai, đệ quy rất hiệu quả khi xử lý các cấu trúc dữ liệu có tính chất lặp lại như cây, danh sách liên kết, hoặc các bài toán toán học như dãy số Fibonacci. Thứ ba, code sử dụng đệ quy thường ngắn gọn và dễ hiểu hơn so với việc sử dụng vòng lặp phức tạp.

Cách hàm đệ quy hoạt động trong Python

Khi một hàm đệ quy được gọi, Python sẽ tạo ra một “khung” mới trong ngăn xếp (stack) để lưu trữ các biến cục bộ và trạng thái của hàm đó. Mỗi lần hàm gọi lại chính nó, một khung mới lại được thêm vào đỉnh ngăn xếp. Quá trình này tiếp tục cho đến khi gặp điều kiện dừng.

Điều kiện dừng (base case) đóng vai trò cực kỳ quan trọng. Nó như một “phanh emergency” ngăn không cho hàm gọi vô hạn. Khi điều kiện dừng được thỏa mãn, hàm sẽ bắt đầu trả về kết quả, và Python sẽ lần lượt “giải phóng” các khung trong ngăn xếp theo thứ tự LIFO (Last In, First Out).

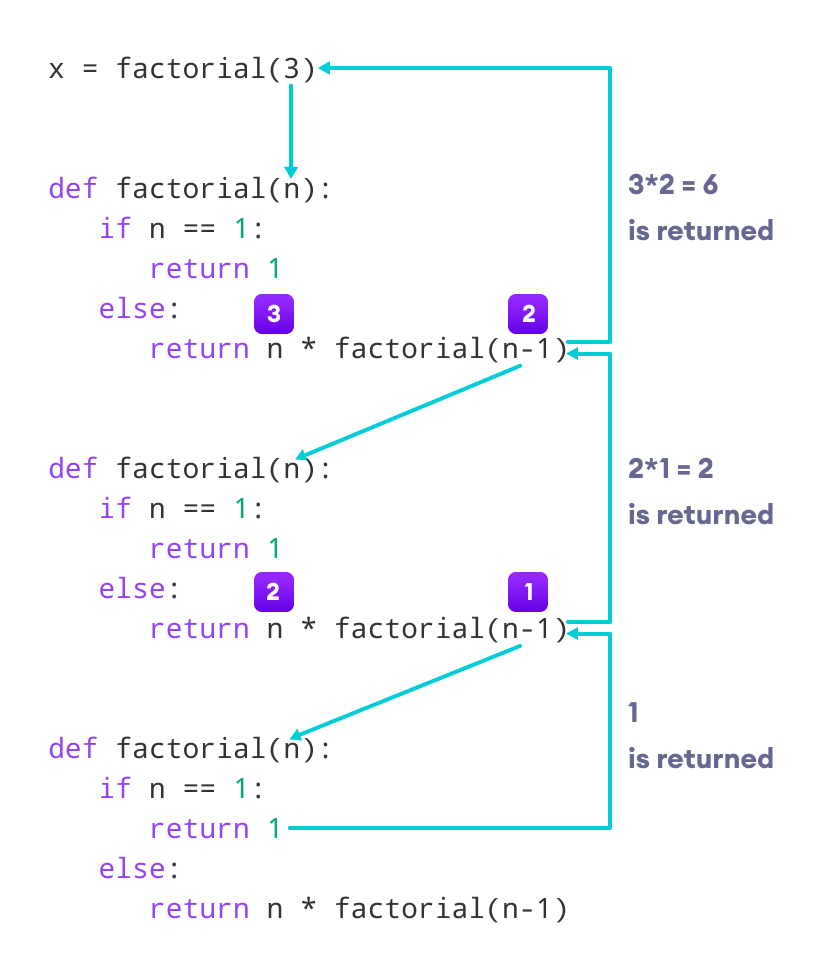
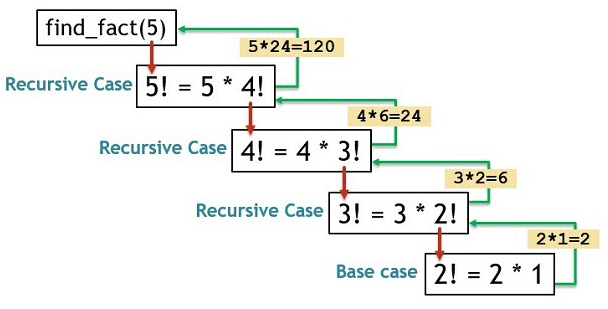
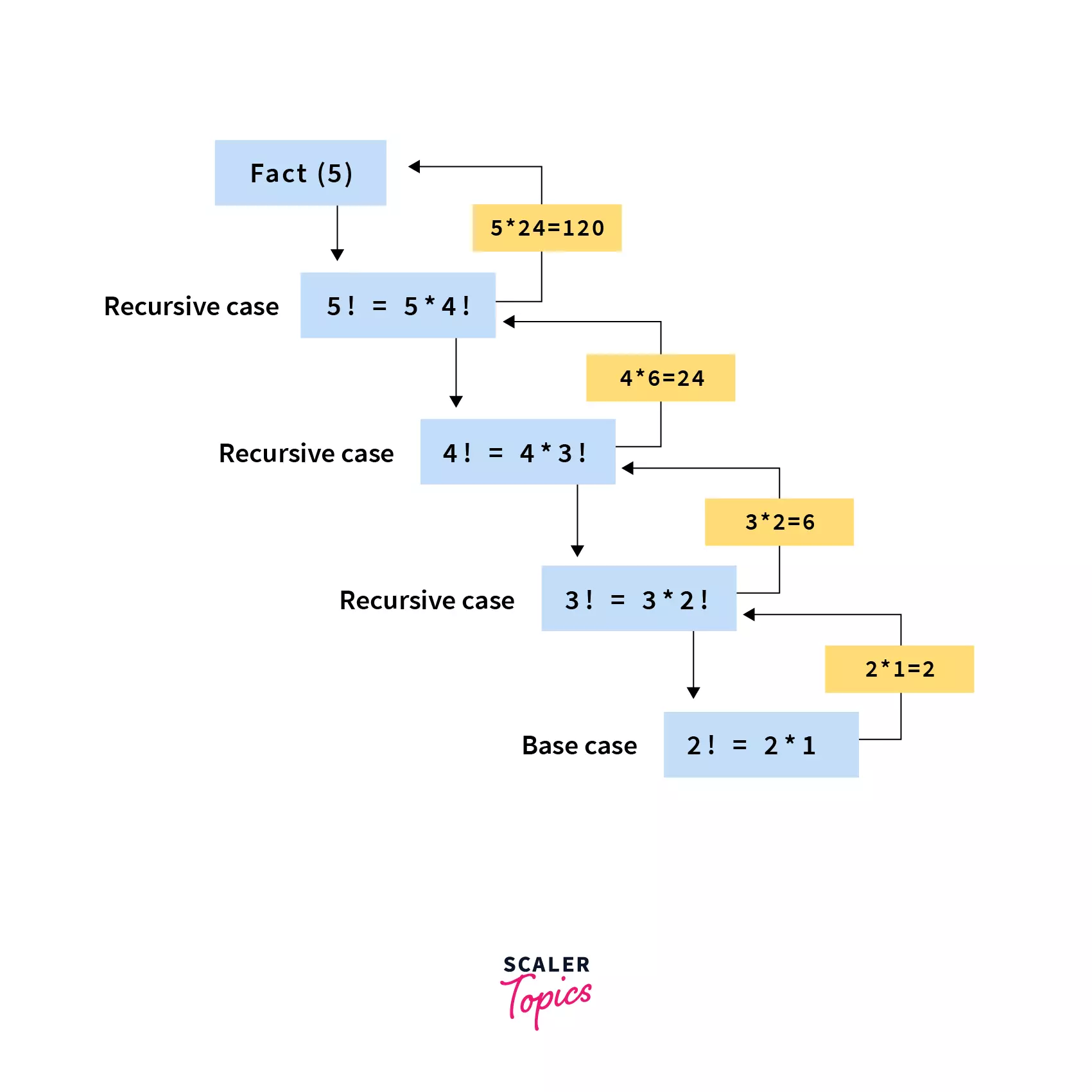
Ví dụ, khi chúng ta tính giai thừa của 5, quá trình sẽ diễn ra như sau: factorial(5) gọi factorial(4), factorial(4) gọi factorial(3), và cứ thế cho đến factorial(1). Sau đó, kết quả được trả về ngược lại: 1 → 2×1=2 → 3×2=6 → 4×6=24 → 5×24=120.

Ví dụ thực tế về đệ quy trong Python

Tính giai thừa bằng đệ quy

Giai thừa là một trong những ví dụ kinh điển nhất để hiểu về đệ quy. Giai thừa của n (ký hiệu n!) được định nghĩa là tích của tất cả các số nguyên dương từ 1 đến n. Chúng ta có thể biểu diễn điều này bằng công thức đệ quy: n! = n × (n-1)!

def factorial(n):
    # Điều kiện dừng: giai thừa của 0 và 1 đều bằng 1
    if n <= 1:
        return 1
    # Gọi đệ quy: n! = n × (n-1)!
    else:
        return n * factorial(n - 1)

# Sử dụng hàm
print(factorial(5))  # Kết quả: 120
print(factorial(0))  # Kết quả: 1

Hãy phân tích từng dòng code này. Dòng đầu tiên kiểm tra điều kiện dừng – nếu n nhỏ hơn hoặc bằng 1, chúng ta trả về 1. Đây là trường hợp cơ sở để ngăn chặn đệ quy vô hạn. Dòng thứ hai thực hiện phép gọi đệ quy, nhân n với giai thừa của (n-1). Khi factorial(5) được gọi, nó sẽ tính 5 × factorial(4), và quá trình này tiếp tục cho đến khi đạt điều kiện dừng.

Tính dãy Fibonacci bằng đệ quy

Dãy Fibonacci là một dãy số nổi tiếng trong toán học, trong đó mỗi số là tổng của hai số trước đó. Dãy bắt đầu với 0, 1 và tiếp tục: 0, 1, 1, 2, 3, 5, 8, 13, 21… Đây là một ví dụ tuyệt vời khác cho đệ quy.

def fibonacci(n):
    # Điều kiện dừng cho các trường hợp cơ sở
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    # Gọi đệ quy: F(n) = F(n-1) + F(n-2)
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

# Sử dụng hàm
for i in range(10):
    print(f"F({i}) = {fibonacci(i)}")

Tuy nhiên, cách tiếp cận đệ quy này có một vấn đề nghiêm trọng về hiệu suất. Hàm fibonacci(n) sẽ tính lại fibonacci(n-1) và fibonacci(n-2), mà fibonacci(n-1) lại phải tính fibonacci(n-2) và fibonacci(n-3). Điều này dẫn đến việc tính toán lặp lại nhiều lần các giá trị giống nhau, làm độ phức tạp thời gian tăng lên cấp số mũ. Với n lớn, chương trình có thể chạy rất chậm hoặc thậm chí bị treo.

Các vấn đề thường gặp khi dùng đệ quy trong Python

Đệ quy vô hạn và lỗi stack overflow

Một trong những lỗi phổ biến nhất khi làm việc với đệ quy là quên hoặc viết sai điều kiện dừng. Khi điều kiện dừng không được thỏa mãn hoặc không bao giờ đạt được, hàm sẽ gọi chính nó vô hạn lần, dẫn đến lỗi “RecursionError” hoặc “maximum recursion depth exceeded”.

def bad_recursion(n):
    # Thiếu điều kiện dừng hoặc điều kiện sai
    print(f"Calling with n = {n}")
    return bad_recursion(n - 1)  # Sẽ gây lỗi RecursionError

# bad_recursion(5)  # Không chạy code này!

Python có cơ chế bảo vệ bằng cách giới hạn độ sâu đệ quy tối đa (mặc định khoảng 1000 lần gọi). Khi vượt quá giới hạn này, Python sẽ ném ra ngoại lệ RecursionError để tránh làm crash chương trình. Bạn có thể kiểm tra và thay đổi giới hạn này bằng module sys, nhưng cần thận trọng vì việc tăng quá nhiều có thể làm cạn kiệt bộ nhớ.

Hiệu suất và giới hạn đệ quy

Mặc dù đệ quy làm code trở nên elegant và dễ hiểu, nó không phải lúc nào cũng là lựa chọn tối ưu về mặt hiệu suất. Mỗi lần gọi hàm đều tạo ra overhead về bộ nhớ và thời gian xử lý. Với những bài toán có thể giải quyết bằng vòng lặp for trong Python đơn giản, đệ quy có thể là “overkill”.

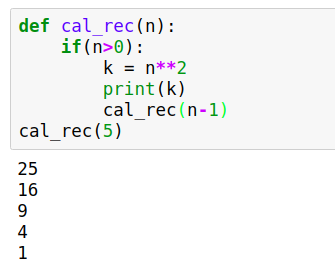
Ví dụ điển hình là hàm Fibonacci đệ quy chúng ta đã thấy ở trên. Với fibonacci(40), hàm sẽ phải thực hiện hàng triệu phép tính, trong khi cách tiếp cận bằng vòng lặp chỉ cần 40 phép tính. Điều này xảy ra vì đệ quy thực hiện nhiều tính toán trùng lặp mà không có cơ chế “nhớ” kết quả đã tính trước đó.

Python cũng có giới hạn về độ sâu ngăn xếp (stack depth). Với các bài toán đòi hỏi hàng nghìn hoặc hàng vạn lần gọi đệ quy, chương trình có thể bị lỗi ngay cả khi logic hoàn toàn đúng. Trong những trường hợp này, giải pháp iterative (vòng lặp) thường là lựa chọn tốt hơn.

Best Practices khi sử dụng đệ quy trong Python

Để sử dụng đệ quy hiệu quả và an toàn, có một số nguyên tắc quan trọng bạn cần ghi nhớ. Đầu tiên và quan trọng nhất, luôn đảm bảo có điều kiện dừng rõ ràng và khả thi. Điều kiện này phải được kiểm tra ngay từ đầu hàm và phải đảm bảo rằng với mọi đầu vào hợp lệ, chúng ta sẽ cuối cùng đạt được điều kiện dừng.

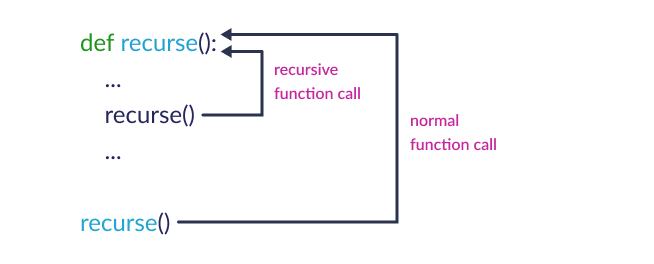
Thứ hai, hãy xem xét kỹ xem đệ quy có thực sự cần thiết không. Nếu bài toán có thể giải quyết bằng vòng lặp đơn giản mà không làm mất tính rõ ràng của code, cách tiếp cận iterative thường tốt hơn về hiệu suất. Đệ quy nên được sử dụng khi nó thực sự làm cho code dễ hiểu hơn, chẳng hạn như khi xử lý cấu trúc dữ liệu cây.

Kỹ thuật memoization (ghi nhớ kết quả) là một cách tuyệt vời để tối ưu hóa các hàm đệ quy bị tính toán trùng lặp. Bạn có thể sử dụng decorator @lru_cache từ module functools của Python:

from functools import lru_cache

@lru_cache(maxsize=None)
def fibonacci_optimized(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci_optimized(n-1) + fibonacci_optimized(n-2)

Cuối cùng, hãy viết code rõ ràng và thêm comment giải thích logic. Đệ quy có thể khó hiểu, đặc biệt là sau một thời gian dài không đọc code. Việc test kỹ lưỡng với các trường hợp biên và input đa dạng cũng rất quan trọng để đảm bảo hàm hoạt động đúng trong mọi tình huống.

Kết luận

Đệ quy là một công cụ mạnh mẽ trong Python giúp chúng ta giải quyết các bài toán phức tạp bằng cách chia nhỏ thành những phần đơn giản hơn. Qua bài viết này, chúng ta đã cùng khám phá từ khái niệm cơ bản, cách thức hoạt động, cho đến những ví dụ thực tế và các vấn đề thường gặp phải khi sử dụng đệ quy.

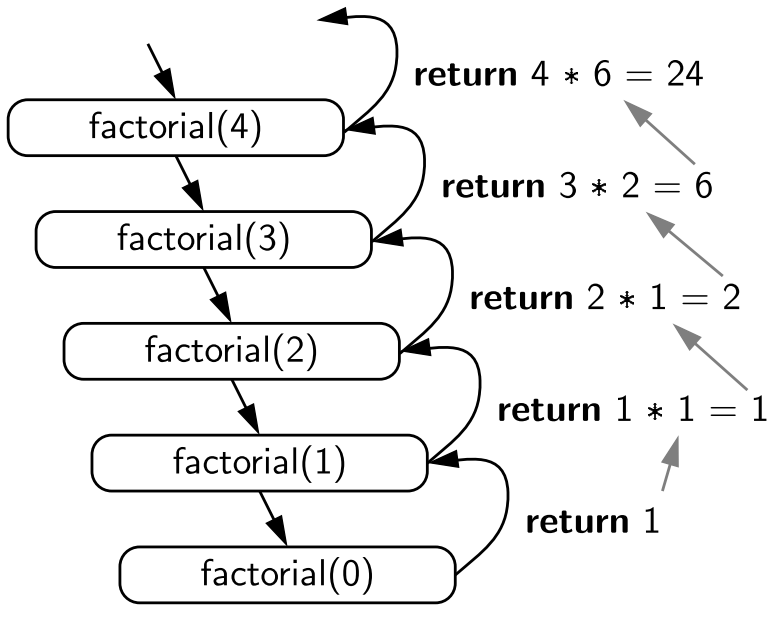
Những điểm quan trọng cần nhớ: đệ quy giúp code trở nên elegant và trực quan, nhưng cần có điều kiện dừng rõ ràng để tránh lỗi vô hạn. Hiệu suất có thể là vấn đề với một số loại đệ quy, nhưng chúng ta có thể tối ưu hóa bằng kỹ thuật memoization hoặc chọn giải pháp iterative khi phù hợp.

Tôi khuyến khích bạn thực hành với các bài toán kinh điển như tính giai thừa, Fibonacci, và dần dần tiến tới những bài toán phức tạp hơn như duyệt cây, thuật toán chia để trị. Hãy nhớ rằng đệ quy không phải là giải pháp cho mọi vấn đề, nhưng khi được sử dụng đúng cách, nó có thể làm cho code trở nên thanh lịch và dễ hiểu hơn rất nhiều.

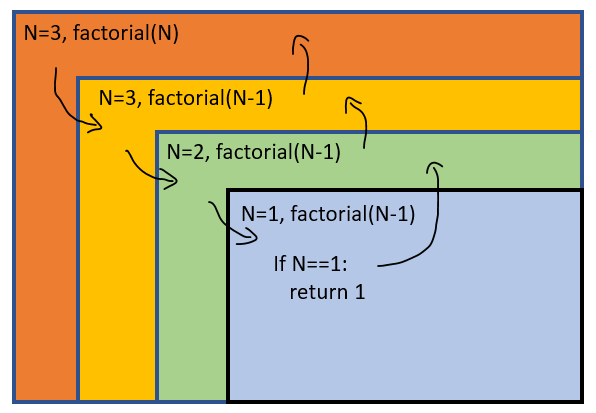
Để tiếp tục hành trình học tập, tôi mời bạn khám phá các kỹ thuật nâng cao khác như đệ quy đa chiều, tail recursion optimization, và các thuật toán divide-and-conquer sử dụng đệ quy. Những kiến thức này sẽ giúp bạn trở thành một lập trình viên Python thành thạo và có thể xử lý những thách thức phức tạp trong các dự án thực tế!

Cũng đừng quên khám phá thêm các kiến thức nền tảng khác như kiểu dữ liệu trong Python, List trong Python hay Set trong Python để xây dựng nền tảng vững chắc cho quá trình học lập trình của bạn.

Cảm ơn bạn đã theo dõi bài viết! Nếu bạn muốn học thêm tài liệu chất lượng về Python, bạn có thể truy cập Chia sẻ Tài liệu học Python để tải về miễn phí.