
Giới thiệu về thứ tự ưu tiên toán tử trong Python
Bạn có bao giờ thắc mắc tại sao biểu thức Python lại trả về kết quả như vậy không? Chẳng hạn như khi viết 2 + 3 * 4, tại sao kết quả lại là 14 thay vì 20? Câu trả lời nằm ở thứ tự ưu tiên toán tử – một khái niệm cơ bản nhưng cực kỳ quan trọng trong lập trình Python.
Thứ tự ưu tiên toán tử quyết định cách Python tính toán biểu thức phức tạp. Nó giống như quy tắc toán học mà chúng ta học từ nhỏ: nhân chia trước, cộng trừ sau. Nhưng trong Python, còn có nhiều loại toán tử khác nữa như so sánh, logic, và gán.
Bài viết này sẽ giải thích thứ tự ưu tiên các toán tử phổ biến, cách xử lý biểu thức, cùng ví dụ minh họa chi tiết. Hiểu rõ kiến thức này sẽ giúp bạn viết code chính xác hơn, tránh được những lỗi logic khó phát hiện.

Tổng quan thứ tự ưu tiên các toán tử phổ biến trong Python
Toán tử số học
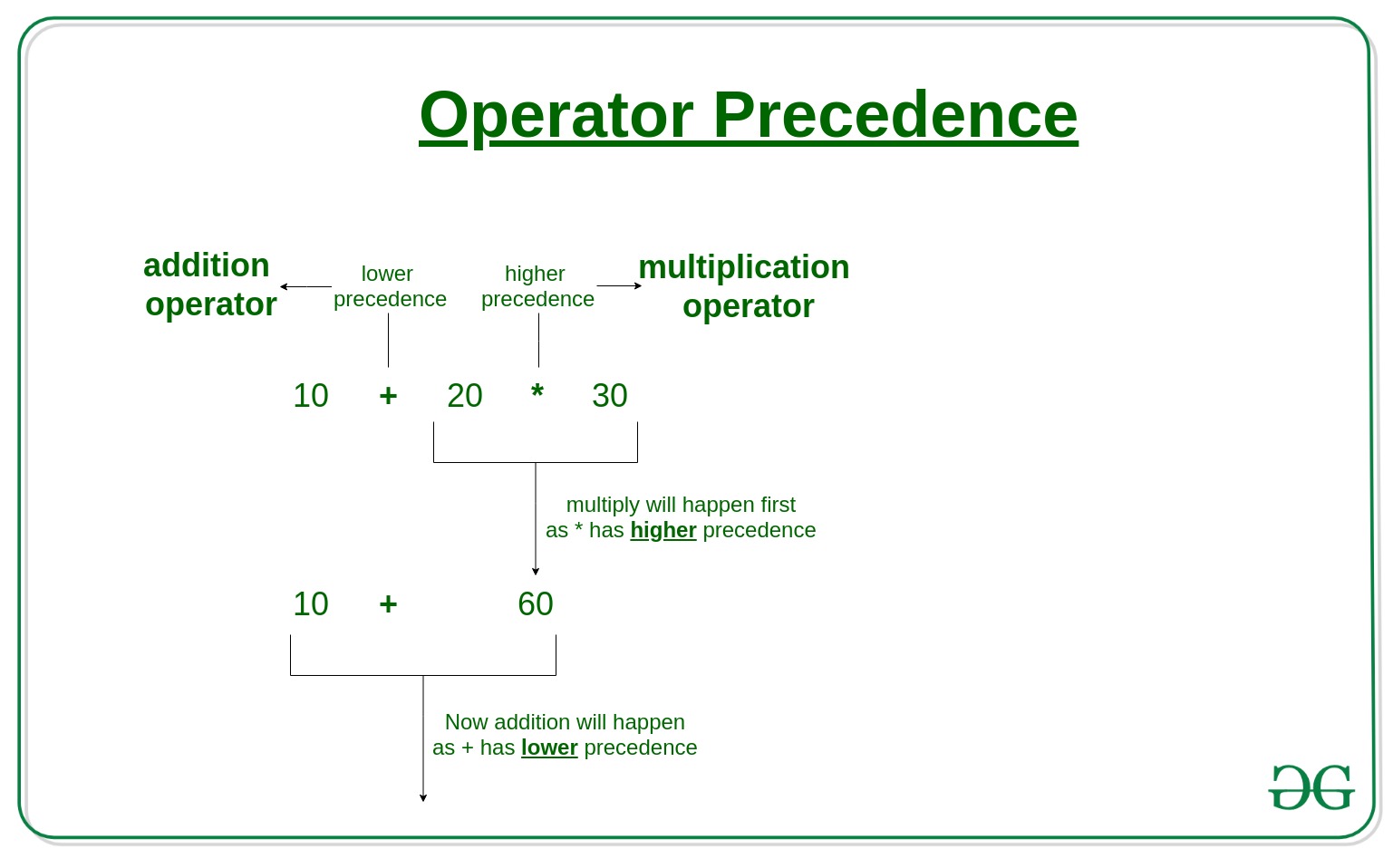
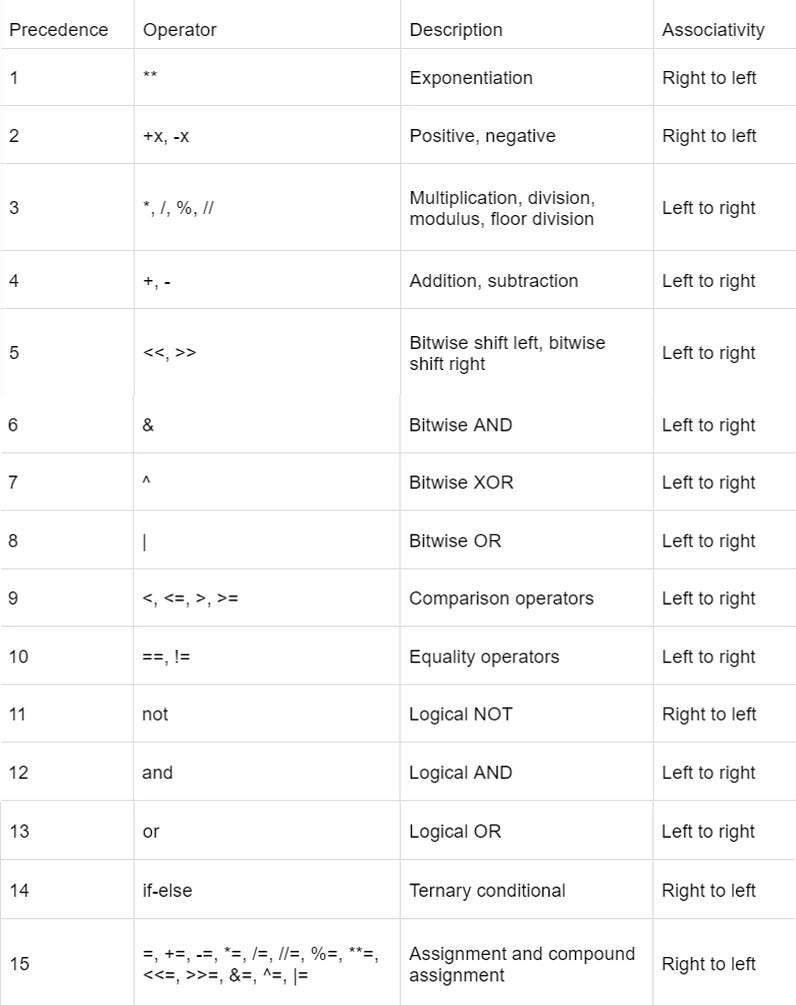
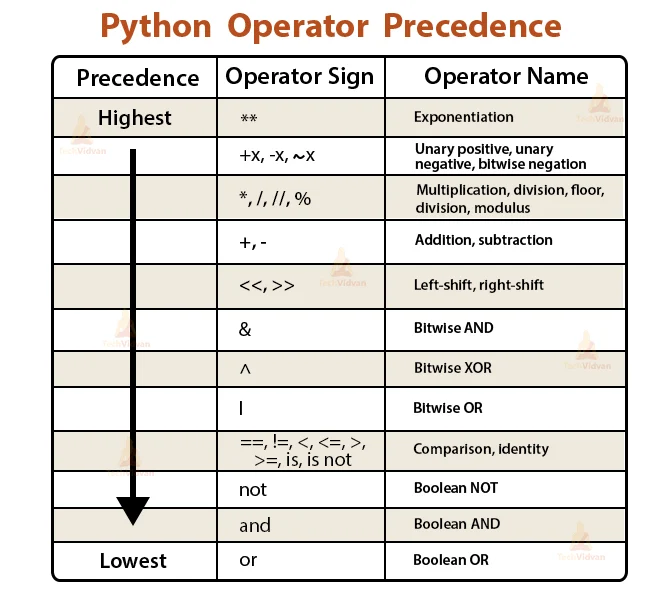
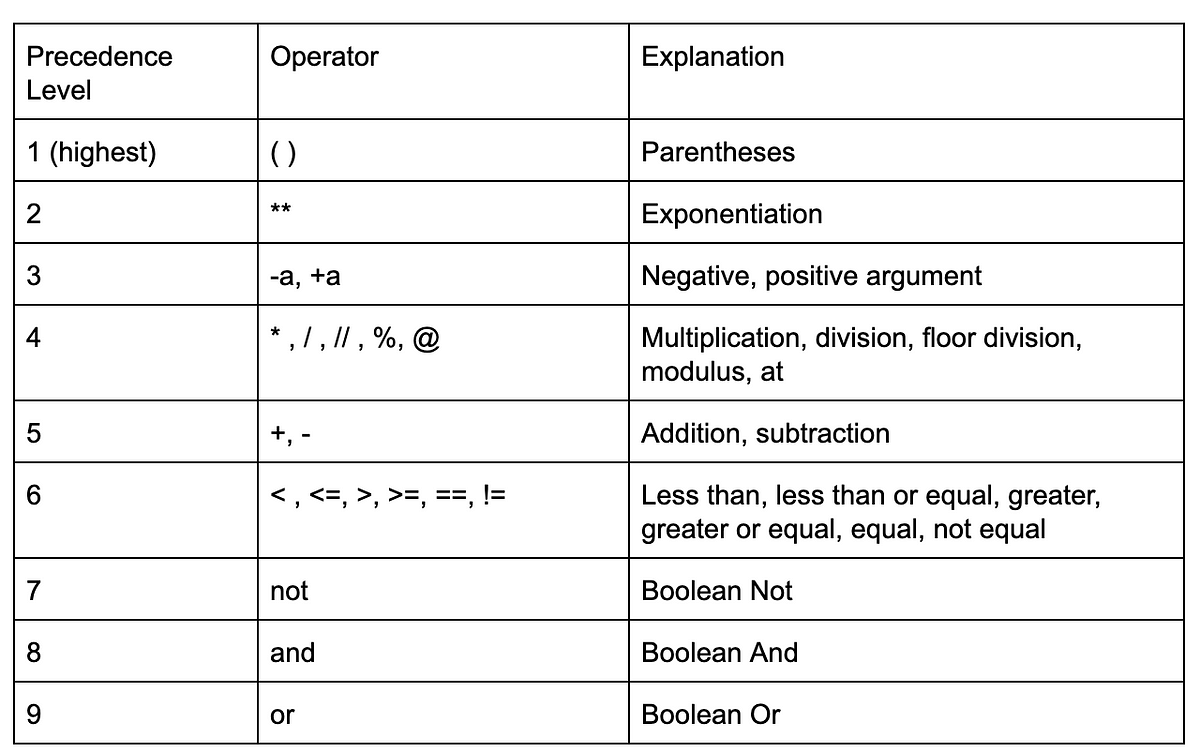
Trong Python, toán tử số học có thứ tự ưu tiên từ cao đến thấp như sau: dấu ngoặc đơn (), toán tử mũ (**), nhân chia (* / // %), và cuối cùng là cộng trừ (+ -). Quy tắc này tương tự như toán học cơ bản mà chúng ta đã quen thuộc.
Hãy xem ví dụ cụ thể: result = 2 + 3 * 4 ** 2. Python sẽ tính theo thứ tự: đầu tiên là 4 ** 2 = 16, sau đó 3 * 16 = 48, và cuối cùng 2 + 48 = 50. Nếu không hiểu rõ thứ tự này, bạn có thể nghĩ kết quả sẽ khác.
Một ví dụ khác với phép chia: a = 10 / 2 * 3. Vì phép nhân và chia có cùng mức ưu tiên, Python sẽ tính từ trái sang phải: 10 / 2 = 5.0, rồi 5.0 * 3 = 15.0. Điều này rất quan trọng khi bạn làm việc với các phép tính phức tạp.
Toán tử so sánh và logic
Toán tử so sánh (<, <=, >, >=, ==, !=) có mức ưu tiên thấp hơn toán tử số học. Điều này có nghĩa là trong biểu thức x + 5 > y * 2, Python sẽ tính x + 5 và y * 2 trước, rồi mới so sánh hai kết quả này.
Toán tử logic (and, or, not) có ưu tiên thấp hơn toán tử so sánh, với not có ưu tiên cao hơn and và or. Khi Python đánh giá điều kiện phức hợp như not False and True or False, nó sẽ thực hiện theo thứ tự: not False (True), sau đó True and True (True), cuối cùng True or False (True).
Việc hiểu rõ thứ tự này giúp bạn viết các điều kiện logic chính xác. Ví dụ: age >= 18 and score > 80 or has_permission sẽ được đánh giá như (age >= 18 and score > 80) or has_permission. Xem thêm hướng dẫn chi tiết về lệnh if trong Python để áp dụng các biểu thức điều kiện hiệu quả.
Toán tử gán
Toán tử gán (=, +=, -=, *=, /=, …) luôn có ưu tiên thấp nhất trong Python. Điều này có nghĩa là mọi phép tính khác sẽ được thực hiện trước khi gán giá trị cho biến.
Khi nào toán tử gán mới được thực hiện? Chỉ sau khi tất cả các toán tử khác đã được xử lý xong. Ví dụ: trong x += y * 2, Python sẽ tính y * 2 trước, rồi cộng kết quả này vào x.
Điều này cũng đúng với các phép gán phức hợp. Trong biểu thức a = b = c + d * 2, Python tính c + d * 2 trước, sau đó gán kết quả cho cả b và a (từ phải sang trái).
Cách xác định thứ tự thực thi biểu thức phức tạp
Kết hợp ưu tiên và liên kết toán tử như thế nào?
Python thực thi toán tử có ưu tiên cao trước, nhưng còn có khái niệm “liên kết” (associativity) ảnh hưởng đến thứ tự tính toán. Hầu hết toán tử trong Python liên kết từ trái sang phải, nghĩa là khi có nhiều toán tử cùng mức ưu tiên, Python sẽ tính từ trái sang phải.
Tuy nhiên, toán tử mũ (**) lại liên kết từ phải sang trái. Ví dụ: 2 ** 3 ** 2 sẽ được tính như 2 ** (3 ** 2) = 2 ** 9 = 512, chứ không phải (2 ** 3) ** 2 = 8 ** 2 = 64. Tham khảo bài viết toàn bộ kiến thức về toán tử trong Python để hiểu sâu về ưu tiên và liên kết toán tử.
Trong biểu thức phức tạp kết hợp số học, logic và gán như result = x > 0 and y + z * 2 < 10, Python sẽ thực hiện theo thứ tự: z * 2, y + (z * 2), x > 0, (y + z * 2) < 10, (x > 0) and ((y + z * 2) < 10), và cuối cùng gán cho result.
Ví dụ chi tiết minh họa thứ tự ưu tiên
Hãy phân tích từng bước biểu thức mẫu: score = base_score + bonus * level ** 2 > passing_grade and attempts < max_attempts. Đây là một biểu thức thực tế có thể xuất hiện trong game hoặc hệ thống chấm điểm.
Bước 1: Python tính level ** 2 (toán tử mũ có ưu tiên cao nhất). Bước 2: Tính bonus * (level ** 2) (phép nhân). Bước 3: Tính base_score + (bonus * level ** 2) (phép cộng). Bước 4: So sánh (base_score + bonus * level ** 2) > passing_grade. Bước 5: So sánh attempts < max_attempts. Bước 6: Thực hiện phép logic (kết quả bước 4) and (kết quả bước 5). Cuối cùng: Gán kết quả cuối cùng cho biến score.
Kết quả trả về sẽ là True hoặc False tùy thuộc vào giá trị các biến. Việc hiểu rõ từng bước này giúp bạn debug và viết code chính xác hơn. Để nâng cao tổng quan về các kiểu dữ liệu tham gia trong biểu thức, bạn có thể xem thêm bài viết về các kiểu dữ liệu trong Python.
Lưu ý về sự khác biệt thứ tự ưu tiên giữa Python và các ngôn ngữ khác
So sánh với C, Java và JavaScript
Một điểm khác biệt quan trọng giữa Python và C/Java là toán tử so sánh chuỗi (chaining comparison). Trong Python, bạn có thể viết 1 < x < 10 và nó hoạt động như mong đợi. Nhưng trong C hay Java, biểu thức tương tự sẽ có nghĩa hoàn toàn khác.
JavaScript có một số quirk (đặc điểm kỳ lạ) về ưu tiên toán tử mà Python không có. Ví dụ, trong JavaScript, true + false cho kết quả 1, nhưng Python sẽ báo lỗi type error.
Một điểm khác nữa là toán tử ** trong Python không tồn tại trong C/Java (họ sử dụng hàm pow()). Nếu bạn quen với những ngôn ngữ này, hãy cẩn thận khi chuyển sang Python.
Tại sao cần hiểu rõ thứ tự ưu tiên riêng của Python?
Hiểu rõ thứ tự ưu tiên Python giúp tối ưu hiệu suất bằng cách viết code hiệu quả hơn. Bạn có thể tránh được việc sử dụng quá nhiều dấu ngoặc không cần thiết, làm code trông gọn gàng hơn.
Nó cũng giúp bạn tránh lỗi lập trình phổ biến, đặc biệt là những lỗi logic khó phát hiện. Khi debug, việc hiểu thứ tự ưu tiên giúp bạn nhanh chóng xác định được vấn đề nằm ở đâu.
Hơn nữa, điều này hỗ trợ đọc và bảo trì mã nguồn dễ dàng hơn. Khi bạn đọc code của người khác (hoặc chính code cũ của mình), hiểu được thứ tự ưu tiên sẽ giúp bạn nắm bắt logic một cách nhanh chóng. Xem thêm bài viết về hàm trong Python để hiểu sâu hơn về cách tổ chức và tối ưu mã nguồn.
Các mẹo sử dụng dấu ngoặc đơn để kiểm soát thứ tự thực thi
Dấu ngoặc đơn có ưu tiên cao nhất trong Python, cho phép bạn kiểm soát hoàn toàn thứ tự tính toán. Công dụng chính của ngoặc đơn là làm rõ ý định của lập trình viên và đảm bảo code hoạt động đúng như mong muốn.
Khi nào nên dùng ngoặc? Hãy dùng khi biểu thức phức tạp hoặc khi bạn không chắc chắn về thứ tự ưu tiên. Thậm chí khi biết rõ thứ tự, việc thêm ngoặc cũng giúp code dễ đọc hơn cho người khác.
Ví dụ thực tế: thay vì viết total_price = base_price + base_price * tax_rate + shipping_fee, hãy viết total_price = base_price + (base_price * tax_rate) + shipping_fee. Mặc dù kết quả giống nhau, nhưng cách viết thứ hai rõ ràng hơn về ý định tính thuế trước.
Vấn đề thường gặp và cách khắc phục
Nhầm lẫn ưu tiên khi dùng nhiều toán tử hỗn hợp
Lỗi phổ biến nhất là nhầm lẫn khi kết hợp nhiều loại toán tử trong cùng biểu thức. Ví dụ: if user_age > 18 and user_score > passing_grade or is_vip có thể không hoạt động như bạn mong đợi nếu không hiểu rõ thứ tự ưu tiên.
Cách kiểm tra và fix lỗi: hãy tách biểu thức thành nhiều phần nhỏ hoặc thêm ngoặc đơn. Trong ví dụ trên, bạn có thể viết: if (user_age > 18 and user_score > passing_grade) or is_vip để làm rõ logic.
Một mẹo hữu ích là sử dụng biến trung gian: thay vì viết biểu thức dài, hãy chia nhỏ thành nhiều bước. Điều này không chỉ dễ đọc mà còn dễ debug hơn.
Hiểu nhầm khi chuyển từ ngôn ngữ khác sang Python
Những lập trình viên từ C/Java thường mắc lỗi khi sử dụng toán tử so sánh chuỗi. Họ có thể viết if (x > 0) and (x < 10) thay vì if 0 < x < 10 – cách viết tự nhiên hơn của Python.
Một thói quen khác gây lỗi là over-parenthesizing – dùng quá nhiều ngoặc đơn không cần thiết. Mặc dù không gây lỗi chương trình, nhưng nó làm code trở nên cumbersome (cồng kềnh) và khó đọc.
Để học đúng cách, hãy đọc code Python của các lập trình viên experienced (có kinh nghiệm) và để ý cách họ sử dụng toán tử. Tài liệu chính thức của Python cũng là nguồn tham khảo đáng tin cậy.

Best Practices khi làm việc với toán tử trong Python
Luôn ưu tiên sự rõ ràng hơn là sự ngắn gọn. Khi biểu thức phức tạp, đừng ngần ngại sử dụng dấu ngoặc đơn để làm rõ ý định. Code dễ đọc hơn code ngắn gọn nhưng khó hiểu.
Hãy hiểu chính xác ưu tiên và liên kết của các toán tử phổ biến. Bạn không cần (và cũng không nên) học thuộc lòng toàn bộ bảng ưu tiên, nhưng những toán tử thường dùng thì cần nắm vững.
Tránh viết biểu thức quá dài hoặc phức tạp trên một dòng. Nếu cần, hãy chia thành nhiều biến trung gian. Điều này không chỉ giúp code dễ đọc mà còn dễ test và debug hơn.
Thường xuyên chạy thử và test kết quả từng phần của biểu thức. Sử dụng Python REPL hoặc Jupyter notebook để experiment (thử nghiệm) với các biểu thức phức tạp trước khi đưa vào code chính.

Kết luận
Thứ tự ưu tiên toán tử là kiến thức nền tảng giúp bạn viết code Python chính xác và hiệu quả. Nó không chỉ giúp tránh những lỗi logic khó phát hiện mà còn làm cho code của bạn professional (chuyên nghiệp) và dễ maintain (bảo trì) hơn.
Không chỉ hiểu lý thuyết, mà việc vận dụng tốt kiến thức này sẽ giúp bạn optimize (tối ưu) logic và giảm thiểu bug trong quá trình phát triển. Hãy nhớ rằng, code tốt không chỉ hoạt động đúng mà còn phải clear (rõ ràng) và understandable (dễ hiểu).
Đừng quên tham khảo tài liệu chính thức của Python để cập nhật kiến thức chuẩn xác nhất. Python liên tục phát triển, và việc theo dõi những thay đổi sẽ giúp bạn luôn cập nhật với best practices mới nhất.
Hãy thử áp dụng ngay hôm nay những kiến thức bạn vừa học được! Bắt đầu với những biểu thức đơn giản, rồi dần dần challenge (thử thách) bản thân với những biểu thức phức tạp hơn. Và đừng quên chia sẻ bài viết này nếu bạn thấy hữu ích – việc sharing (chia sẻ) kiến thức luôn mang lại giá trị cho cộng đồng lập trình viên Việt Nam!

Để hỗ trợ học tập bài bản hơn, bạn có thể tải kho tài liệu học Python miễn phí do Bùi Mạnh Đức chia sẻ.









