Trong thế giới lập trình, việc sắp xếp dữ liệu là một trong những tác vụ cơ bản và quan trọng nhất. Từ việc hiển thị danh sách sản phẩm theo giá đến việc xử lý các tập dữ liệu lớn, chúng ta luôn cần đến các thuật toán sắp xếp. Bạn đã bao giờ tự hỏi làm thế nào máy tính có thể sắp xếp hàng triệu bản ghi chỉ trong chớp mắt chưa? Câu trả lời nằm ở việc sử dụng các thuật toán hiệu quả. Trong đó, QuickSort nổi lên như một trong những giải pháp mạnh mẽ và được sử dụng rộng rãi nhất. Nó được xem là “con dao pha” của các thuật toán sắp xếp nhờ tốc độ vượt trội trong hầu hết các trường hợp. Bài viết này sẽ cùng bạn tìm hiểu chi tiết về QuickSort, từ định nghĩa, nguyên lý hoạt động, các bước thực hiện, ưu nhược điểm, cho đến những ứng dụng thực tế và cách tối ưu hóa hiệu suất của nó.
QuickSort là gì? Tổng quan về thuật toán QuickSort
Để bắt đầu, hãy cùng làm quen với khái niệm cốt lõi của thuật toán sắp xếp này và tìm hiểu về lịch sử ra đời của nó.
Định nghĩa QuickSort
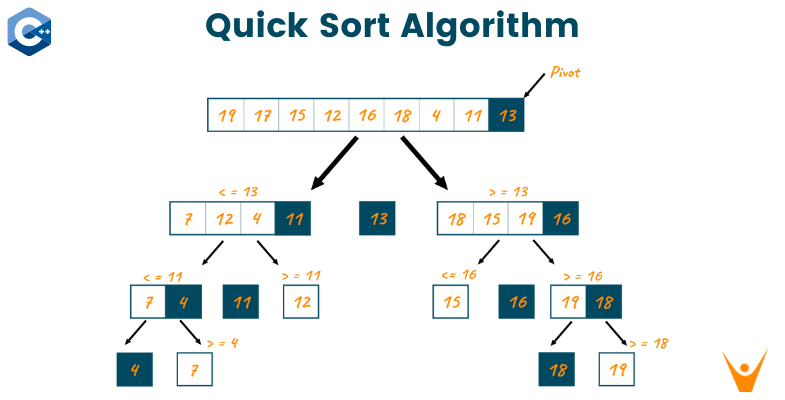
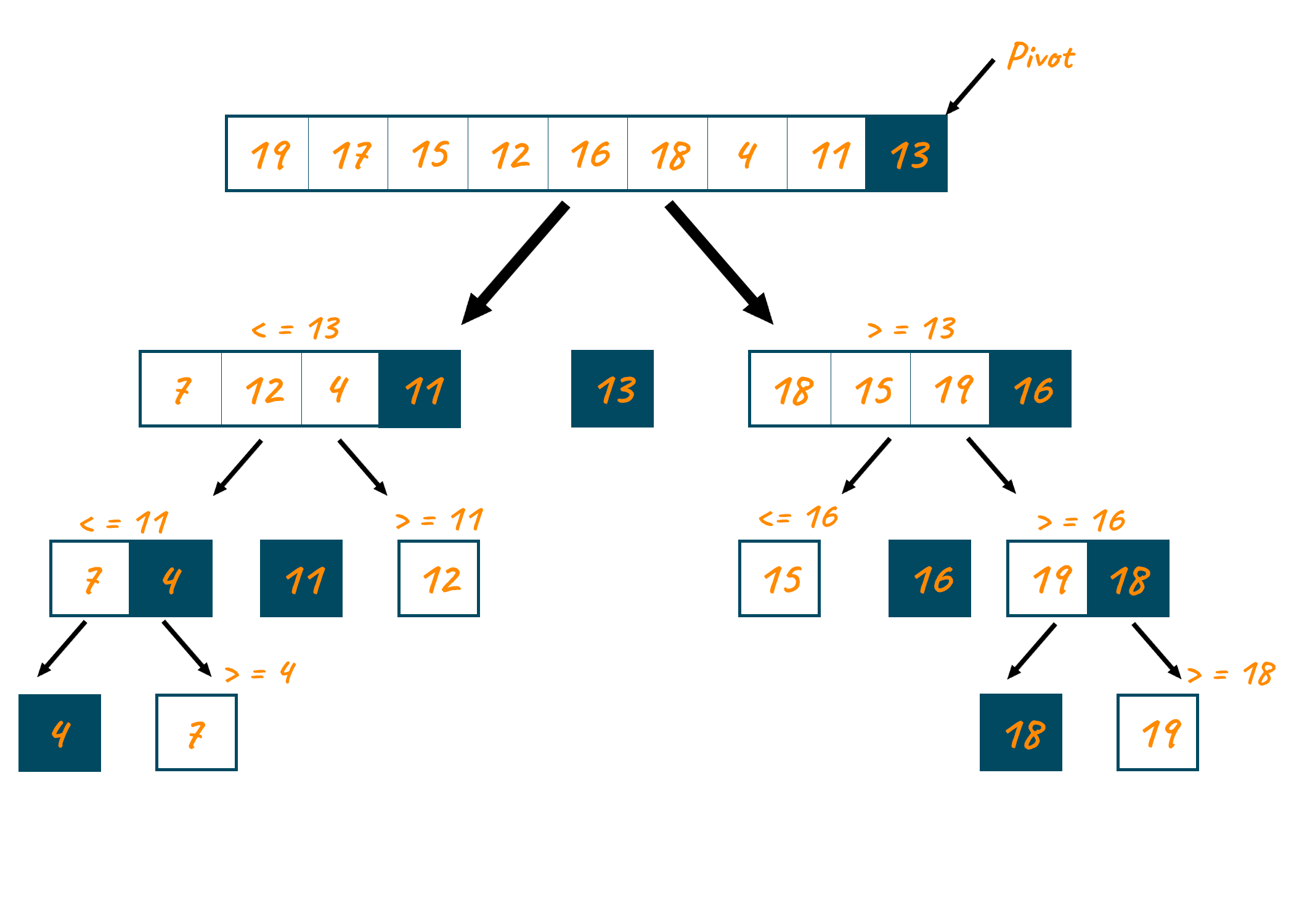
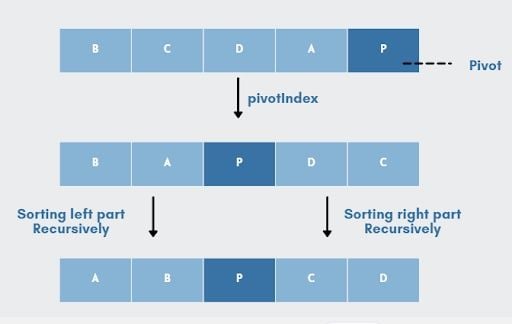
QuickSort, hay còn gọi là thuật toán sắp xếp nhanh, là một thuật toán sắp xếp hiệu quả hoạt động dựa trên chiến lược “chia để trị” (Divide and Conquer). Ý tưởng chính của nó là chọn một phần tử trong mảng làm “pivot” (điểm tựa), sau đó phân vùng các phần tử khác trong mảng thành hai nhóm: một nhóm chứa các phần tử nhỏ hơn pivot và một nhóm chứa các phần tử lớn hơn pivot. Quá trình này được lặp lại đệ quy cho các mảng con cho đến khi toàn bộ mảng được sắp xếp hoàn chỉnh.
Nhờ cách tiếp cận này, QuickSort có thể đạt được hiệu suất rất cao, đặc biệt với các tập dữ liệu lớn. Nó được coi là một trong những thuật toán sắp xếp nhanh nhất hiện nay cho các tác vụ thông thường.

Lịch sử và nguồn gốc QuickSort
QuickSort được phát minh bởi nhà khoa học máy tính người Anh, Tony Hoare, vào năm 1959 khi ông đang làm việc tại Đại học Quốc gia Moscow. Ban đầu, Hoare phát triển thuật toán này để giải quyết bài toán dịch một kho từ vựng từ tiếng Nga sang tiếng Anh, nhằm tối ưu hóa quá trình tra cứu. Ông nhận ra rằng việc sắp xếp các từ trước sẽ tăng tốc đáng kể cho việc tìm kiếm. QuickSort ra đời từ nhu cầu thực tế đó và nhanh chóng chứng tỏ được sự ưu việt của mình. Kể từ đó, nó đã trở thành một trong những thuật toán sắp xếp phổ biến và được dạy rộng rãi trong khoa học máy tính, đồng thời được tích hợp vào thư viện chuẩn của nhiều ngôn ngữ lập trình hiện đại.
Nguyên lý hoạt động của QuickSort dựa trên phương pháp chia để trị
Sức mạnh của QuickSort đến từ một nguyên lý rất thông minh: chia để trị. Hãy cùng phân tích sâu hơn về cách thuật toán này áp dụng ý tưởng đó để giải quyết bài toán sắp xếp một cách hiệu quả.
Ý tưởng chia để trị trong QuickSort
Chia để trị là một chiến lược giải quyết vấn đề bằng cách phân rã một bài toán lớn thành các bài toán con nhỏ hơn, dễ giải quyết hơn. Sau khi các bài toán con được giải quyết, kết quả của chúng sẽ được kết hợp lại để tạo thành lời giải cho bài toán ban đầu. QuickSort áp dụng nguyên lý này một cách hoàn hảo:
1. Chia (Divide): Mảng ban đầu được phân vùng thành hai mảng con. Quá trình này được thực hiện bằng cách chọn một phần tử làm pivot. Tất cả các phần tử nhỏ hơn hoặc bằng pivot được chuyển sang bên trái pivot, và tất cả các phần tử lớn hơn pivot được chuyển sang bên phải.
2. Trị (Conquer): Thuật toán QuickSort được gọi đệ quy để sắp xếp hai mảng con này một cách độc lập.
3. Kết hợp (Combine): Vì các mảng con được sắp xếp “tại chỗ” (in-place), nên không cần bước kết hợp nào cả. Khi các lời gọi đệ quy kết thúc, toàn bộ mảng ban đầu đã được sắp xếp.

Cách chọn pivot và phân vùng (partition)
Việc chọn pivot và thực hiện phân vùng là trái tim của thuật toán QuickSort. Hiệu suất của thuật toán phụ thuộc rất nhiều vào bước này.
Vai trò của pivot: Pivot là phần tử tham chiếu để chia mảng. Sau bước phân vùng, pivot sẽ đứng đúng vị trí của nó trong mảng đã được sắp xếp. Có nhiều cách để chọn pivot:
- Chọn phần tử đầu tiên hoặc cuối cùng: Đây là cách đơn giản nhất nhưng có thể dẫn đến hiệu suất kém nếu mảng đã được sắp xếp hoặc gần sắp xếp.
- Chọn phần tử ngẫu nhiên: Cách này giúp giảm khả năng gặp phải trường hợp xấu nhất, làm cho thuật toán trở nên ổn định hơn.
- Chọn phần tử trung vị của ba (median-of-three): Lấy ba phần tử (thường là đầu, giữa và cuối), và chọn phần tử có giá trị ở giữa làm pivot. Đây là một kỹ thuật phổ biến để tránh các trường hợp xấu nhất.
Quá trình phân vùng (Partitioning): Sau khi chọn pivot, quá trình phân vùng sẽ sắp xếp lại mảng. Một phương pháp phân vùng phổ biến (Lomuto partition scheme) hoạt động như sau: Di chuyển pivot đến cuối mảng. Dùng một con trỏ `i` để theo dõi ranh giới của vùng chứa các phần tử nhỏ hơn pivot. Duyệt qua mảng, nếu gặp phần tử nhỏ hơn pivot, hãy hoán đổi nó với phần tử tại vị trí `i` và tăng `i` lên. Cuối cùng, hoán đổi pivot (đang ở cuối) với phần tử tại `i` để đặt pivot vào đúng vị trí cuối cùng của nó.
Các bước thực hiện thuật toán QuickSort
Bây giờ, hãy cùng hệ thống lại toàn bộ quy trình hoạt động của QuickSort qua từng bước cụ thể và một ví dụ minh họa trực quan để bạn dễ dàng hình dung.
Mô tả thuật toán theo từng bước
Thuật toán QuickSort có thể được tóm gọn trong ba bước chính, được lặp đi lặp lại một cách đệ quy:
Bước 1: Chọn Pivot
Đầu tiên, bạn cần chọn một phần tử từ mảng để làm pivot. Như đã đề cập, có nhiều chiến lược chọn pivot như chọn phần tử đầu, cuối, ngẫu nhiên hoặc trung vị của ba. Lựa chọn pivot thông minh là chìa khóa để đảm bảo hiệu suất tốt.
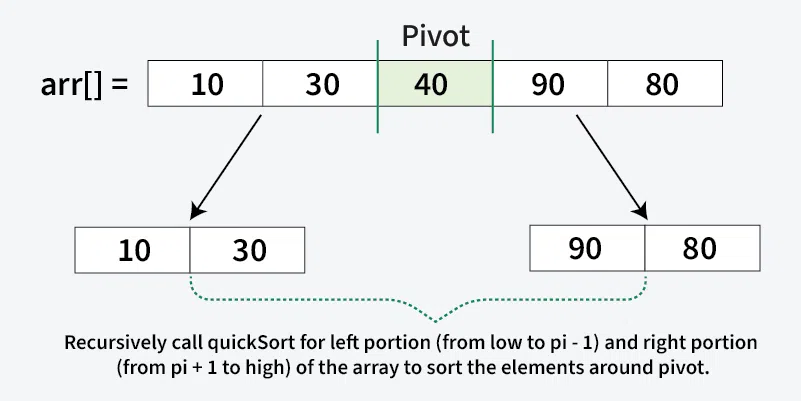
Bước 2: Phân vùng (Partition)
Sắp xếp lại mảng sao cho tất cả các phần tử nhỏ hơn pivot được đặt trước pivot, và tất cả các phần tử lớn hơn pivot được đặt sau nó. Sau bước này, pivot sẽ nằm ở vị trí chính xác của nó trong mảng cuối cùng. Các phần tử bằng pivot có thể nằm ở một trong hai bên.
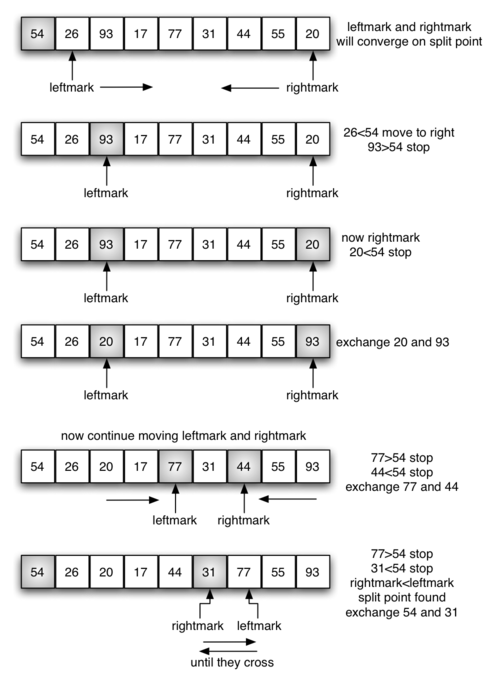
Bước 3: Đệ quy sắp xếp các phần con
Sau khi phân vùng, mảng được chia thành hai mảng con (một bên trái và một bên phải của pivot). Thuật toán QuickSort sau đó được gọi đệ quy cho từng mảng con này. Quá trình này tiếp tục cho đến khi mảng con chỉ còn một phần tử hoặc không có phần tử nào, lúc đó nó được coi là đã được sắp xếp.
Ví dụ minh họa cụ thể
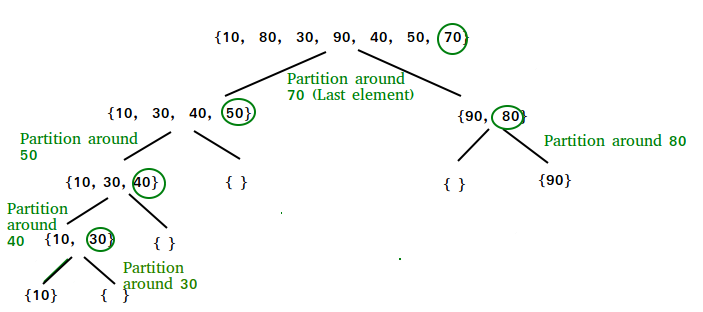
Để hiểu rõ hơn, chúng ta hãy xem xét một ví dụ với mảng số nguyên: `[8, 3, 1, 7, 0, 10, 2]`.
Lần 1: Mảng ban đầu `[8, 3, 1, 7, 0, 10, 2]`
- Chọn pivot: Giả sử ta chọn phần tử cuối cùng làm pivot, tức là `pivot = 2`.
- Phân vùng: Ta sắp xếp lại mảng. Các phần tử nhỏ hơn 2 (`0, 1`) được đưa về bên trái. Các phần tử lớn hơn 2 (`8, 3, 7, 10`) được đưa về bên phải. Mảng trở thành `[0, 1, 2, 7, 8, 10, 3]`. Pivot `2` đã ở đúng vị trí.
Lần 2: Sắp xếp đệ quy hai mảng con
- Mảng con bên trái: `[0, 1]`. Mảng này đã được sắp xếp (hoặc có thể chạy thêm một bước nữa để xác nhận).
- Mảng con bên phải: `[7, 8, 10, 3]`.
Lần 3: Sắp xếp mảng con `[7, 8, 10, 3]`
- Chọn pivot: Chọn phần tử cuối cùng làm pivot, `pivot = 3`.
- Phân vùng: Không có phần tử nào nhỏ hơn 3. Các phần tử lớn hơn 3 (`7, 8, 10`) được đưa về bên phải. Mảng trở thành `[3, 8, 10, 7]`. Pivot `3` đã ở đúng vị trí.
Tiếp tục đệ quy:
- Mảng con bên trái của `3` là rỗng.
- Mảng con bên phải của `3` là `[8, 10, 7]`.
Quá trình này tiếp tục cho đến khi tất cả các mảng con được sắp xếp. Cuối cùng, mảng ban đầu sẽ trở thành `[0, 1, 2, 3, 7, 8, 10]`.
Ưu điểm và hạn chế của thuật toán QuickSort
Giống như bất kỳ công cụ nào, QuickSort có những điểm mạnh vượt trội nhưng cũng đi kèm với một số hạn chế cần lưu ý. Hiểu rõ cả hai mặt sẽ giúp bạn quyết định khi nào nên và không nên sử dụng nó.
Ưu điểm nổi bật của QuickSort
1. Hiệu suất trung bình rất cao
QuickSort có độ phức tạp thời gian trung bình là O(n log n), đây là một trong những mức hiệu suất tốt nhất cho các thuật toán sắp xếp dựa trên so sánh. Trong thực tế, với các tập dữ liệu lớn và ngẫu nhiên, QuickSort thường chạy nhanh hơn các thuật toán O(n log n) khác như Thuật toán sắp xếp MergeSort hay HeapSort nhờ vào hằng số thấp trong công thức độ phức tạp và khả năng tận dụng tốt bộ nhớ cache.

2. Sử dụng bộ nhớ hiệu quả (In-place)
Một trong những lợi thế lớn nhất của QuickSort là nó là một thuật toán sắp xếp “tại chỗ” (in-place). Điều này có nghĩa là nó chỉ cần một lượng bộ nhớ phụ rất nhỏ, với độ phức tạp không gian là O(log n) để quản lý các lời gọi đệ quy trên stack. So với MergeSort, vốn yêu cầu O(n) bộ nhớ phụ để lưu trữ mảng tạm, QuickSort tiết kiệm bộ nhớ hơn rất nhiều, làm cho nó trở thành lựa chọn lý tưởng cho các hệ thống có bộ nhớ hạn chế.
Hạn chế và nhược điểm cần lưu ý
1. Hiệu suất kém trong trường hợp xấu nhất
Trường hợp xấu nhất của QuickSort xảy ra khi việc chọn pivot luôn dẫn đến sự phân vùng không cân bằng. Ví dụ, nếu bạn luôn chọn phần tử nhỏ nhất hoặc lớn nhất làm pivot (thường xảy ra với mảng đã được sắp xếp hoặc sắp xếp ngược), mảng sẽ bị chia thành một mảng con có `n-1` phần tử và một mảng con rỗng. Khi đó, độ phức tạp thời gian sẽ suy biến thành O(n²), tương đương với các thuật toán chậm như Bubble Sort. Mặc dù hiếm gặp với chiến lược chọn pivot tốt, đây vẫn là một rủi ro cần xem xét.
2. Vấn đề về đệ quy sâu có thể gây tràn bộ nhớ stack (Stack Overflow)
Vì QuickSort sử dụng đệ quy, mỗi lời gọi hàm sẽ chiếm một không gian trên bộ nhớ stack. Với các tập dữ liệu cực lớn, độ sâu của cây đệ quy có thể trở nên quá lớn, dẫn đến lỗi tràn bộ nhớ stack. Vấn đề này có thể được giảm thiểu bằng các kỹ thuật tối ưu hóa như đệ quy đuôi (tail recursion) hoặc sử dụng phiên bản lặp (iterative) của QuickSort, nhưng nó vẫn là một hạn chế cố hữu của cách triển khai đệ quy đơn giản. Để tìm hiểu sâu hơn về các kỹ thuật gỡ lỗi và tối ưu, bạn có thể tham khảo bài viết Debug là gì.
Ứng dụng thực tế của QuickSort trong lập trình và kỹ thuật sắp xếp
Với hiệu suất vượt trội, QuickSort không chỉ là một khái niệm lý thuyết mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực của ngành công nghệ phần mềm.
Ứng dụng trong các ngôn ngữ lập trình phổ biến
QuickSort là một lựa chọn hàng đầu để triển khai chức năng sắp xếp mặc định trong thư viện chuẩn của nhiều ngôn ngữ lập trình. Tốc độ trung bình nhanh và việc sử dụng bộ nhớ hiệu quả khiến nó trở thành một giải pháp rất thực tế.
- Trong C: Hàm thư viện `qsort()` chính là một triển khai của QuickSort.
- Trong Java: Lớp `Arrays` sử dụng một phiên bản QuickSort được tối ưu hóa (dual-pivot QuickSort) để sắp xếp các kiểu dữ liệu nguyên thủy (như int, float).
- Trong Python: Hàm `sort()` và `sorted()` sử dụng một thuật toán lai gọi là Timsort, nhưng trong nhiều triển khai CPython cũ hơn hoặc trong các thư viện khác, Introsort (một thuật toán lai giữa QuickSort, HeapSort và Insertion Sort) được sử dụng để tận dụng tốc độ của QuickSort mà vẫn đảm bảo hiệu suất O(n log n) trong trường hợp xấu nhất. Nếu bạn muốn tìm hiểu thêm, hãy đọc bài Python là gì để hiểu sâu hơn về cách ngôn ngữ này hỗ trợ các thuật toán.
Ứng dụng trong xử lý dữ liệu và thuật toán khác
Ngoài các thư viện chuẩn, QuickSort còn là nền tảng cho nhiều tác vụ phức tạp hơn:
1. Xử lý cơ sở dữ liệu: Các hệ quản trị cơ sở dữ liệu thường cần sắp xếp một lượng lớn các bản ghi để thực hiện các truy vấn (ví dụ: `ORDER BY`). QuickSort là một ứng cử viên sáng giá cho các tác vụ này khi dữ liệu có thể được nạp vào bộ nhớ. Bạn có thể đọc thêm về SQL là gì và cách dữ liệu được quản lý ở cấp độ cơ sở dữ liệu.
2. Chuẩn hóa dữ liệu đầu vào: Nhiều thuật toán yêu cầu dữ liệu đầu vào phải được sắp xếp trước khi xử lý. Ví dụ, thuật toán tìm kiếm nhị phân (Binary Search) chỉ hoạt động trên một tập dữ liệu đã được sắp xếp. QuickSort thường được sử dụng như một bước tiền xử lý hiệu quả.
3. Tìm phần tử lớn thứ k: Một biến thể của QuickSort, được gọi là Quickselect, có thể tìm thấy phần tử lớn thứ k (hoặc nhỏ thứ k) trong một tập hợp với độ phức tạp trung bình chỉ là O(n), nhanh hơn nhiều so với việc sắp xếp toàn bộ mảng.
So sánh QuickSort với các thuật toán sắp xếp khác
Để đánh giá đúng giá trị của QuickSort, điều quan trọng là phải đặt nó bên cạnh các thuật toán sắp xếp phổ biến khác. Việc so sánh này sẽ cho thấy rõ điểm mạnh và điểm yếu của từng phương pháp.
QuickSort vs MergeSort
Đây là hai “gã khổng lồ” trong thế giới thuật toán sắp xếp O(n log n). Cả hai đều dựa trên nguyên lý chia để trị nhưng có những khác biệt quan trọng:
- Tốc độ thực tế: Mặc dù cả hai đều có độ phức tạp trung bình là O(n log n), QuickSort thường nhanh hơn MergeSort trong thực tế. Lý do là QuickSort có hằng số thấp hơn và tận dụng tốt hơn bộ nhớ cache của CPU do tính chất sắp xếp tại chỗ.
- Sử dụng bộ nhớ: QuickSort là thuật toán in-place, chỉ cần O(log n) không gian bộ nhớ phụ cho stack đệ quy. Ngược lại, MergeSort yêu cầu O(n) không gian phụ để tạo các mảng tạm, gây tốn kém bộ nhớ hơn đáng kể.
- Hiệu suất trường hợp xấu nhất: MergeSort luôn đảm bảo độ phức tạp O(n log n) trong mọi trường hợp. QuickSort có thể suy giảm xuống O(n²) nếu chọn pivot kém, mặc dù điều này hiếm khi xảy ra với các phiên bản được tối ưu.
- Tính ổn định (Stability): MergeSort là một thuật toán sắp xếp ổn định, nghĩa là nó giữ nguyên thứ tự tương đối của các phần tử có giá trị bằng nhau. QuickSort nguyên bản thì không ổn định.
QuickSort vs Bubble Sort và Selection Sort
So sánh QuickSort với các thuật toán cơ bản như Bubble Sort (sắp xếp nổi bọt) hay Selection Sort (sắp xếp chọn) cho thấy một sự khác biệt một trời một vực về hiệu năng.
- Độ phức tạp: QuickSort có độ phức tạp trung bình O(n log n), trong khi cả Bubble Sort và Selection Sort đều có độ phức tạp là O(n²). Sự khác biệt này trở nên cực kỳ lớn khi kích thước mảng (n) tăng lên.
- Tính thực tiễn: Với một mảng 1 triệu phần tử, QuickSort có thể hoàn thành trong vài giây, trong khi Bubble Sort hoặc Selection Sort có thể mất hàng giờ hoặc thậm chí hàng ngày. Do đó, Bubble Sort và Selection Sort chỉ mang tính giáo khoa hoặc chỉ hữu ích cho các tập dữ liệu rất nhỏ, còn QuickSort là lựa chọn thực tiễn cho hầu hết các ứng dụng trong thế giới thực.
Common Issues/Troubleshooting
Mặc dù mạnh mẽ, QuickSort vẫn có thể gặp phải một số vấn đề về hiệu suất nếu không được triển khai cẩn thận. Dưới đây là các sự cố thường gặp và cách khắc phục chúng.
QuickSort bị chậm hoặc tệ nhất khi nào?
Vấn đề lớn nhất của QuickSort là hiệu suất có thể giảm đột ngột từ O(n log n) xuống O(n²). Tình huống này được gọi là “trường hợp xấu nhất” và thường xảy ra do chọn pivot không hợp lý.
Nguyên nhân:
Trường hợp xấu nhất xảy ra khi pivot được chọn luôn là phần tử nhỏ nhất hoặc lớn nhất trong mảng (hoặc mảng con). Điều này khiến quá trình phân vùng trở nên mất cân bằng nghiêm trọng: một bên có `n-1` phần tử và bên còn lại không có phần tử nào. Điều này thường xảy ra khi:
- Mảng đầu vào đã được sắp xếp hoặc sắp xếp ngược.
- Tất cả các phần tử trong mảng đều bằng nhau.
Cách phòng tránh:
Chìa khóa để tránh trường hợp xấu nhất là chọn pivot một cách thông minh hơn.
- Pivot ngẫu nhiên (Random Pivot): Chọn một phần tử ngẫu nhiên làm pivot. Điều này làm cho khả năng liên tục gặp phải trường hợp xấu nhất trên cùng một đầu vào là cực kỳ thấp.
- Trung vị của ba (Median-of-Three): Chọn ba phần tử (thường là đầu, giữa, cuối), sau đó chọn phần tử có giá trị ở giữa làm pivot. Kỹ thuật này gần như loại bỏ hoàn toàn khả năng mảng đã được sắp xếp trở thành trường hợp xấu nhất.
Vấn đề đệ quy quá sâu gây stack overflow
Vì QuickSort là một thuật toán đệ quy, mỗi lần gọi hàm đệ quy sẽ tiêu tốn một phần bộ nhớ trên call stack. Nếu mảng đầu vào quá lớn, cây đệ quy có thể trở nên rất sâu, dẫn đến lỗi tràn bộ nhớ stack.
Giải pháp tối ưu:
- Tối ưu hóa đệ quy đuôi (Tail Call Optimization): Một số trình biên dịch có thể tối ưu hóa các lời gọi đệ quy đuôi thành một vòng lặp, giúp tiết kiệm không gian stack. Bạn nên ưu tiên đệ quy trên mảng con nhỏ hơn trước để giảm độ sâu tối đa của stack.
- Sử dụng phiên bản lặp (Iterative QuickSort): Có thể triển khai QuickSort bằng cách sử dụng một vòng lặp và một stack tường minh (do người dùng quản lý) thay vì đệ quy. Cách này tránh được giới hạn của call stack hệ thống.
- Thuật toán lai (Hybrid Algorithm): Kết hợp QuickSort với thuật toán khác. Ví dụ, Introsort chuyển sang HeapSort nếu độ sâu đệ quy vượt quá một ngưỡng nhất định để đảm bảo độ phức tạp O(n log n) và tránh stack overflow.
Best Practices
Để khai thác tối đa sức mạnh của QuickSort và giảm thiểu rủi ro, hãy áp dụng các thực hành tốt nhất sau đây khi triển khai và sử dụng thuật toán này.
1. Chọn pivot thông minh
Đây là quy tắc quan trọng nhất. Tránh các chiến lược chọn pivot đơn giản như luôn chọn phần tử đầu tiên hoặc cuối cùng. Thay vào đó, hãy sử dụng phương pháp “trung vị của ba” (median-of-three) hoặc chọn một pivot ngẫu nhiên. Điều này giúp ngăn ngừa hiệu suất suy giảm xuống O(n²) trên các tập dữ liệu đặc biệt như mảng đã được sắp xếp. Bạn có thể tham khảo thêm Algorithm optimization để biết các kỹ thuật tối ưu thuật toán hiệu quả.
2. Áp dụng khi dữ liệu lớn, kết hợp với Insertion Sort cho mảng nhỏ
QuickSort hoạt động hiệu quả nhất trên các tập dữ liệu lớn. Tuy nhiên, đối với các mảng con rất nhỏ (ví dụ, dưới 10-20 phần tử), chi phí của các lời gọi đệ quy có thể lớn hơn lợi ích mà nó mang lại. Một kỹ thuật tối ưu phổ biến là tạo ra một thuật toán lai: khi một mảng con trong quá trình đệ quy trở nên đủ nhỏ, hãy chuyển sang dùng Insertion Sort (sắp xếp chèn) để sắp xếp nó. Insertion Sort rất hiệu quả với các mảng nhỏ và có hằng số thấp.
3. Cẩn trọng xử lý dữ liệu đã gần như được sắp xếp
Nếu bạn biết dữ liệu đầu vào của mình thường đã được sắp xếp hoặc gần sắp xếp, việc chọn pivot đơn giản (như phần tử cuối) sẽ là một sai lầm. Hãy đảm bảo chiến lược chọn pivot của bạn đủ mạnh mẽ để xử lý các trường hợp này, chẳng hạn như sử dụng pivot ngẫu nhiên.
4. Không nên để QuickSort chạy đệ quy quá sâu
Để tránh nguy cơ tràn bộ nhớ stack, hãy giới hạn độ sâu của đệ quy. Một phương pháp hiệu quả là Introsort: nó bắt đầu bằng QuickSort, nhưng nếu độ sâu đệ quy vượt quá một ngưỡng nhất định (thường là `2 * log(n)`), nó sẽ chuyển sang HeapSort. HeapSort đảm bảo độ phức tạp O(n log n) và không phải là thuật toán đệ quy, giúp ngăn chặn trường hợp xấu nhất của QuickSort một cách an toàn.
Conclusion
Qua bài viết này, chúng ta đã cùng nhau khám phá sâu sắc về QuickSort – một trong những thuật toán sắp xếp mạnh mẽ và phổ biến nhất trong khoa học máy tính. Chúng ta đã thấy rằng sức mạnh của nó nằm ở nguyên lý “chia để trị” thông minh, mang lại hiệu suất trung bình O(n log n) ấn tượng và khả năng sắp xếp tại chỗ giúp tiết kiệm bộ nhớ. Tuy nhiên, nó cũng có những điểm yếu như hiệu suất O(n²) trong trường hợp xấu nhất và nguy cơ tràn bộ nhớ stack, nhưng những vấn đề này hoàn toàn có thể được kiểm soát bằng các kỹ thuật tối ưu thông minh như chọn pivot ngẫu nhiên hay sử dụng thuật toán lai.
Với sự cân bằng giữa tốc độ, hiệu quả sử dụng tài nguyên và tính linh hoạt, QuickSort xứng đáng là một công cụ không thể thiếu trong bộ kỹ năng của bất kỳ lập trình viên là gì nào. Đừng ngần ngại áp dụng nó vào các dự án của bạn để giải quyết các bài toán sắp xếp một cách hiệu quả. Để nâng cao hơn nữa kỹ năng của mình, bạn có thể tìm hiểu thêm về các thuật toán sắp xếp khác như MergeSort, HeapSort hay Timsort để có cái nhìn toàn diện và lựa chọn được giải pháp tối ưu nhất cho từng tình huống cụ thể.









